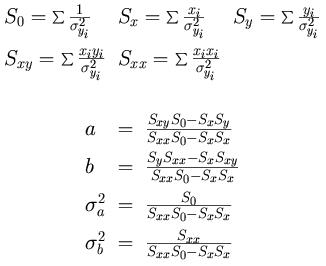
N L_1 eL_1 T_1 eT_1 L_2 eL_2 T_2 eT_2 ... L_N eL_N T_N eT_N(dove L=lunghezza in m, eL=errore su L, T=periodo, eT=errore sul periodo)
T2 = (4 pi2)/g L
dove a=(4 pi2)/g e b=0.Soluzione analitica del metodo dei minimi quadrati (trascurando l'errore sulle x):
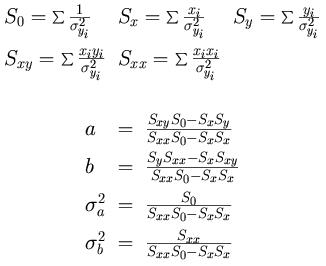
void minquadrati(int n, double *x, double *y, double *ex, double *ey, double &a, double &b, double &ea, double &eb)
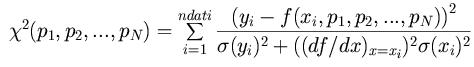
int ndat;
double *x,*y,*ex,*ey;
#define npar 2
double fchiq(int n, double *xpar){
// calcolo del chi-quadro
// valore di ritorno = valore del chi-quadro
}
int main(){
double par[npar]={val_1,val_2,...,val_npar}; // valori dei param. da cui iniziare
// la minimizzazione
double outpar[npar],err[npar],chiq;
R_MinuitSimpl(fchiq,npar,par,outpar,err,&chiq);
// outpar -> valore dei parametri in corrispodenza del minimo
// err -> errore sui parametri
// chiq -> valore della funzione nel minimo
return 0
}
Applicare ai dati dell'esercizio precedente la soluzione numerica del metodo
dei minimi quadrati prima trascurando poi considerando il contributo dell'errore su x
(termine con la derivata al denominatore).
N t1 et1 L1 eL1 t2 et2 L2 eL2 ... tN etN LN eLN(t=tempo in sec.,L=elongazione in cm).
f(x,p1,p2,p3) = p1*exp(-p2*t)*cos(p3*t)(trascurate l'errore sul tempo)
nome_funzione numero_parametri valore_iniziale_1 passo_1 minimo_1 massimo_1 ... valore_iniziale_n passo_n minimo_n massimo_n numero_punti x_1 y_1 ex_1 ey_1 ... x_m y_m ex_m ey_mIl programma dovrà essere strutturato in funzioni che realizzino i principali task:
string fun_name;
double (*fun)(double x, double *par);
...
if (fun_name == "retta") {
fun = retta;
} else if (fun_name == "esponenziale") {
fun = esponenziale;
} ...
} else {
cout << } EXIT(-1); FUNZIONE NON DISPONIBILE << ENDL;