Scopo di questa esercitazione èleggere dei dati da un file, riempire
un istogramma e confrontare la distribuzione
dei dati sperimentali con una funzione.
Lettura da file e riempimento istogramma
Confronto con una distribuzione teorica
Lettura da file
e riempimento istogramma
Leggete i dati sperimentali da uno dei file che abbiamo preparato (
m1.dat,
m2.dat,
m3.dat).
Questi dati simulano una serie di misure affette da errore statistico
e quindi sono distribuiti secondo una distribuzione gaussiana (da verificare!).
Potrà essere utile avere come variabili accessibili da tastiera il
numero di bin e gli estremi del grafico (facoltativamente potreste calcolarveli
automaticamente dai dati).
1) Ogni volta che leggete un dato, inseritelo (Fill) in
un istogramma precedentemente inizializzato. L'istogramma stesso sarà
il contenitore dei
vostri dati per cui evitate l'uso di vettori.
2) Leggendo i dati calcolate la media e la varianza. Per il calcolo
di quest'ultima dovete usare la formula seguente che vi permette di calcolare
la varianza senza dover conoscere il valore della media quando calcolate
il contributo i-esimo.
&sigma2 = <x2> - <x>2
3) A lettura ultimata, estraete dal vostro grafico i valori di media
e varianza utilizzando le formule
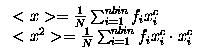
4) Provate il vostro programma usando come input i 3 file di dati.
Confronto con
una distribuzione teorica
Per fare il confronto con una distribuzione teorica si puo' procedere
in due modi: sovrapporre all'istogramma dei dati sperimentali la funzione
teorica opportunamente normalizzata oppure sovrapporre ai dati un istogramma
"teorico". Questo confronto è ovviamente solo qualitatitivo.
Per proseguire vi servirà quindi una funzione del tipo (esempio nel
caso di distribuzione gaussiana)
double gauss (double *x, double* par){
par[0]=normalizzazione;
par[1]=media;
par[2]=rms;
... calcolo della gaussiana...
}
che utilizzerete per inizializzare un oggetto della classe TF1.
Sovrapposizione della funzione teorica
Sovrapponete all'istogramma dei dati la funzione
teorica.
Questa andrà opportunamente normalizzata infatti
la densità di probabilità ha integrale 1, mentre l'integrale dell'istogramma
dei dati ha integrale NΔx, dove Δx è la larghezza
di ogni bin.
Sovrapposizione dell'istogramma teorico
Sovrapponete all'istogramma dei dati un istogramma
che riempirete mettendo in ogni bin il numero di entries valutato utilizzando
la densità
di probabilità. Per il bin centrato su xc, il
numero di eventi atteso vale NΔx p(xc). Il riempimento di ciascun bin dell'istogramma
si puo' fare
con un'unica chiamata ad Fill usando xc come
x e NΔx p(xc) come peso (dove p è la densità di probabilità e Δx p(xc)
è il valore approssimato dell'area della densità di probabilità nel
bin con centro xc). Dovrete quindi implementare un loop:
for (i=1; i<=nbin;i++){
xc = ... calcolo del centro del bin i....
... riempimento del bin i...
}
Fit
Infine utilizzate un fit per ottenere media e rms dai dati sperimentali e ripetete il confronto utilizzando uno dei due metodi precedenti. Un modo semplice per fittare la la densità di probabilità p(x) consiste nel fittare la funzione gauss fissando a 1 la normalizzazione.