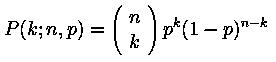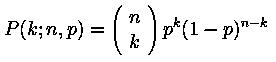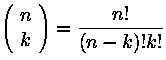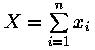Terza Esercitazione (Generazione di numeri casuali)
Esercizio 1
Esercizio 2
Esercizio 3
Nota: utilizzate la rappresentazione con istogrammi per la visualizzazione di tutte le distribuzioni che intervengono nell'esercitazione.
Esercizio 1
Utilizzare la funzione random() (che ritorna numeri interi casuali (aleatori) tra 0 e RAND_MAX ) per generare numeri distribuiti uniformemente nell'intervallo [0,1]. Generalizzare a l'intervallo [xmin,xmax].
Visualizzare la distribuzione dei valori generati.
Esercizio 2
Simulare N ripetizioni di n prove indipendenti ciascuna con probabilit` di successo p: 0< p< 1 (lancio di una moneta, tavolo binario, etc..).
Confrontare la distribuzione del numero di successi k (0<= k<= n) con la distribuzione teorica (binomiale)
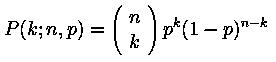
Strutturare il programma utilizzando le seguenti funzioni
- int binEvent(double p, int n);
simuli n prove indipendenti ciascuna con probabilit` p e ritorni il numero di successi k (0<= n succ <= n)
- int/double binCoeff(int n, int k);
calcolo del coefficiente binomiale
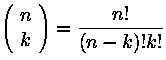
(attenzione al modo in cui si fa il calcolo: facile perdere precision e/o eccedere i limiti delle variabili intere)
- double binomiale(double p, int n, int k);
Calcolo della probabilit` di k successi per n prove di probabilit` p
Fare un fit della distribuzione simulata con la distribuzione teorica con parametro libero p .
(Facoltativo - necessario per Laboratorio di Fisica) Confrontare anche con la distribuzione gaussiana fittando media e deviazione standard (attenzione alla scelta degli intervalli: il centro dell'intervallo deve coincidere con un valore intero perché il confronto abbia senso).
Esercizio 3
Il teorema del limite centrale afferma che la distribuzione di n variabili aleatorie, per n sufficientemente grande, tende alla distribuzione gaussiana.
Simulare N "estrazioni" di X
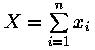
con x i variabili aleatorie distribuite uniformemente tra [-0.5,0.5].
Si esegua un fit alla distribuzione di X cosl ottenuta con una funzione gaussiana verificando che x med =0 e sigma=sqrt(n/12).
Verificare che l'accordo tra distribuzione simulata e gaussiana migliora al crescere di n (provare n=2,6,12).
Per n=12 X h una variabile aleatoria distribuita secondo una gaussiana di media 0 e deviazione standard 1.
Scrivere una funzione che generare variabili aleatorie distribuite secondo una gaussiana di media x0 e deviazione standard sigma.