par[0]= normalizzazione;
par[1]=x0
par[2]=σ
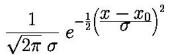
par[0]=normalizzazione
par[1]=λ
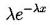
In questa esercitazione genereremo, a partire da numeri uniformente
distribuiti, numeri casuali distribuiti
secondo una distribuzione f(x) qualunque.
In particolare useremo la funzione gaussiana e la funzione esponenziale,
per cui vi consigliamo di crearvi inizialmente le due funzioni:
| double gauss (double *x, double *par) par[0]= normalizzazione; par[1]=x0 par[2]=σ |
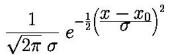
|
| double esp (double *x, double *par) par[0]=normalizzazione par[1]=λ |
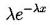
|
Nota: per verificare che i numeri estratti siano effettivamente distribuiti
secondo le funzioni desiderate, utilizzate la rappresentazione con istogrammi per la visualizzazione
di tutte le distribuzioni Montecarlo e teoriche
che intervengono nell'esercitazione.
Per avere un confronto quantitativo, realizzate almeno un fit di una
distribuzione simulata a vostra scelta.
Per il fit dell'istogramma provate ad utilizzate il metodo Fit
(che costruisce per voi la funzione di chi quadro). Trovate
qui un esempio.
Esercizio 1
Esercizio 2
Esercizio 3
Esercizio 1
Generazione di numeri distribuiti secondo una funzione f(x)
utilizzando il metodo di reiezione (potete provare sia la gaussiana che l'esponenziale).
- Estrazione di un singolo numero della sequenza: scegliete opportunamente
fmax,
xmin e xmax, quindi estraete una coppia di numeri random (x,y) uniformemente distribuiti
nella regione [xmin,xmax]x[0,fmax]
finche' non e' verificata la condizione y<f(x). Il valore
ottenuto x e' allora un numero della sequenza desiderato.
Per implementare questo algoritmo, potete utilizzare una funzione che
ritorna un elemento della sequenza del tipo:
double reiezione(double fmax, double xmin, double xmax)
- Ripetere l'estrazione fino ad ottenere N numeri della sequenza e verificare che siano effettivamente distribuiti secondo f(x) (sovrapponendo gli istogrammi o facendo il fit).
- Calcolare il rapporto tra le estrazioni accettate e quelle effettuate
al variare degli estremi (fmax,xmin,xmax).
Notate che questo rapporto moltiplicato per l'area del rettangolo di
estrazione e' pari all'integrale di f(x) tra xmin e xmax.
Esercizio 2
Generazione di numeri distribuiti secondo la funzione f(x) utilizzando
il metodo di inversione.
Ricordate che il metodo e' valido solo per funzioni integrabili (provate
ad implementarlo con la funzione esponenziale).
Notate che con questo metodo, per ogni estrazione di un numero uniformemente
distribuito, si ottiene un numero della sequenza desiderato.
- Trovate, secondo il metodo di inversione, la trasformazione x
= g(η).
g e' una funzione tale che, se η e'
distribuita uniformemente in [0,1], allora g(η)
e' distribuita secondo la distribuzione di probabilità
f(x) nell'intervallo [xmin,xmax].
g(η) si ricava risolvendo l'equazione
η = &intxxmin f(w) dw
Implementate una funzione che ritorna un elemento della funzione:
double inversione();
- Estraete N numeri e verificate che siano effettivamente distribuiti
secondo f(x) (sovrapponendo gli istogrammi o facendo il fit).
Esercizio 3
Generazione di numeri distribuiti secondo una gaussiana utilizzando
il metodo della gaussiana bidimensionale.
Questo metodo permette, a partire da due numeri η1
e
η2distribuiti uniformemente,
di ottenere due numeri x e y distribuiti gaussianamente:
u = - log(1-η1)
r = sqrt(2u)
q = 2πη2
x = rcos(q)
y = rsin(q)
- Implementate una funzione che calcoli un singolo elemento della sequenza. Per farlo in maniera efficiente, dovete fare il calcolo di x e y una volta ogni due chiamate della funzione seguendo per esempio questo schema:
double gaussiana2D(){
static double x,y;
static int flag = 0;
if (flag==0){
// calcolo x e y una volta ogni due chiamate
flag=1;
return x;
} else {
flag = 0;
return y;
}
}
- Estraete N numeri random e e verificate che siano distribuiti secondo una gaussiana con media 0 e deviazione standard 1 (sovrapponendo gli istogrammi o facendo il fit).
- Generalizzate l'algoritmo per generare numeri distribuiti secondo una gaussiana con media e deviazione standard qualunque (sovrapponendo gli istogrammi o facendo il fit)..
double fitfunc(double *x, double *par){
// funzione con cui eseguire il fit
}
int main(){
...
TF1 f("func",fitfunc,xmin,xmax,npar); // crea l'oggetto TF1 associato alla funzione
f.SetParameters(par) // inizializza il vettore di parametri
h.Fit("func"); // h e' un oggetto della classe TH1D
// le funzioni piu' diffuse possono essere utilizzate direttamente senza creare una TF1 (vedi manuale)
...
}