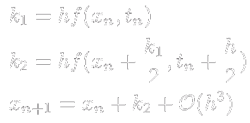
| Introduzione |
Questa esercitazione affronta la soluzione numerica delle equazioni differenziali ordinarie.
Dopo aver impostato un algoritmo atto a risolvere una generica
equazione differenziale di secondo grado (metodo di Runge-Kutta)
lo applicherete alla soluzione dell'equazione del moto di un corpo
disegnandone la traettoria.
Esercizio 1
Esercizio 2
Esercizio 3
Applicazione di RK al second'ordine
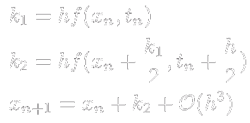
all'oscillatore smorzato
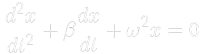
soluzione analitica:
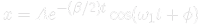
dove
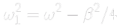
Provate il caso beta=0 e beta=1 entrambi con omega=4.
Confrontate il risultato numerico con
la soluzione analitica.
Ripetete il punto 1. utilizzando RK al quart'ordine.
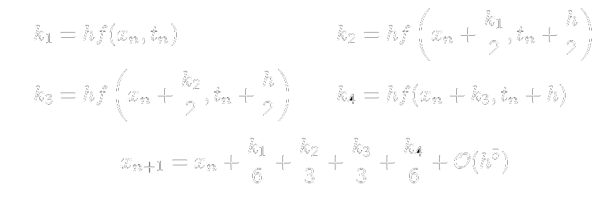
Affrontate uno di questi due problemi (facoltativo)
Come disegnare punti in movimento
Modifica di un grafico
Può essere utile poter modificare un grafico aggiungendo nuovi punti o
modificando le coordinate di quelli già esistenti. Ad esempio quando calcolare
numericamente x in funzione di t può essere utile aggiornare il grafico
ogni volta che il punto viene calcolato in modo da controllarne l'andamento.
...
// valore iniziale
double t0=0.0;
double x0=...;
TGraph gr(1,&t0,&x0); // definisco un grafico contenente un solo punto
gr.SetMarkerStyle(20); // definisco lo stile di punto associato
gr.Draw("AP"); // disegno il grafico (con calcolo automatico degli assi)
for (...){
double t = ...;
double x = ...; // risultato del calcolo numerico..;
gr.SetPoint(i,t,x); // aggiungo un nuovo punto al grafico
c.Modified(); // forzo l'aggiornamento (Update) della finestra
c.Update(); // "dicendo" che in essa ci sono oggetti modificati (Modified)
}
...
Traettoria 2D
Supponiamo di voler disegnare la traettoria di un punto
nel piano x-y facendo "muovere" il punto.
...
// valori iniziali
double t0=0.0;
double x0=...,double y0=...;
TGraph gr(1,&x0,&y0); // definisco un grafico contenente un solo punto
gr.SetMarkerStyle(20); // definisco lo stile di punto associato
gr.Draw("AP"); // disegno il grafico (con calcolo automatico degli assi)
for (int i=1;i<100;i++){
double t = ...;
double x = ...; // risultato del calcolo numerico..
double y = ...; // risultato del calcolo numerico..
gr.SetPoint(0,x,y); // cambio le coordinate del punto
c.Modified(); // forzo l'aggiornamento (Update) della finestra
c.Update(); // "dicendo" che in essa ci sono oggetti modificati (Modified)
}
...
Come noterete eseguendo questo codice il punto è sempre al centro del grafico
(gli assi vengono ricalcolati automaticamente).
Se si vuole che gli assi siano fissi
(utile per visualizzare meglio la traettoria) occorre fissare gli estremi del grafico
ad ogni disegno; ad es. se fissiamo gli estremi a [-3,3]x[-2,2] bisogna aggiungere
prima di c.Modified(); il seguente codice:
gr.GetXaxis()->SetLimits(-3,3); gr.SetMaximum(2); gr.SetMinimum(-2);Grafici 3D
...
TView view(1); // Creo un sistema di assi cartesiani (1)
view.SetRange(-2,-2,0,2,2,10); // Fisso gli estremi [-2,2]x[-2,2]x[0,10]
view.ShowAxis(); // Si devono vedere gli assi
// valore iniziale
double t0=0.0;
double x0=...;
double y0=...;
double z0=...;
TPolyMarker3D gr(1); // Creo un grafico 3d fatto da un solo punto
gr.SetPoint(0,x0,y0,z0); // e ne fisso le coordinate
gr.SetMarkerStyle(20); // Definisco lo stile di punto associato
gr.Draw(); // Disegno il grafico
for (int i=1;i<1000;i++){
double t = t0+i*0.1;
double x = ...; // risultato del calcolo numerico..
double y = ...; // risultato del calcolo numerico..
double z = ...; // risultato del calcolo numerico..
gr.SetPoint(0,x,y,z); // Aggiorno le coordinate
c.Modified(); // forzo l'aggiornamento (Update) della finestra
c.Update(); // "dicendo" che in essa ci sono oggetti modificati (Modified)
}
...